Цилиндр в математике, площадь и объем

Понятие цилиндр в математике включается в изучение темы «Тела вращения». Как правило, школьники неплохо усваивают данную тему. Большую роль играет знакомство с цилиндром школьников, так как ученики уже в старших классах готовятся к профессиональной деятельности и практике в жизни.

Многие предметы из жизни имеют форму цилиндра.

Цилиндр в математике школы

В школе стереометрия изучается школьниками обычно по материалу, основанному на следующих темах:

• стереометрические аксиомы и следствия из них;
• понятие параллельности прямых и плоскостей в пространстве, а так же их свойства;
• понятия перпендикулярности прямых и плоскостей в пространстве, а так же их свойства;
• понятия векторов и координата, их свойств, а также геометрических преобразований в пространстве;
• понятия геометрического тела, а именно многогранников и тел вращений, их свойств;
• понятия площади поверхности и объема геометрических тел, а так же их измерение и вычисление;
• построение многогранников и тел вращения на плоскости.

Например, потребуется нам рассчитать объем ведра или какой-либо другой емкости, имеющей форму цилиндра.

Итак, давайте рассмотрим, что же такое цилиндр?

Под такой пространственной фигурой мы будем понимать тело, которое составляется из 2 кругов и отрезков, соединяющих эти круги. Причем круги находятся в плоскостях, параллельных друг другу, а отрезки соединяют соответственные их точки.

Такие отрезки мы будем называть образующими, а круги – основаниями. Тело имеет свой радиус. Он соответствует радиусам кругов, из которых оно составлено. Как мы уже сказали, основания фигуры – круги, параллельные друг другу.

Добавим еще то, что они равны. Так же и все образующие тела равны и параллельны друг другу. У этой фигуры также есть поверхность. Будем называть ее цилиндрической. Эта поверхность составляется из боковой, образованной поворотом образующей тела вокруг его оси, и его оснований – кругов.

Под высотой этого тела вращения мы будем понимать расстояние между его кругами – основаниями. А прямую линию, которая соединяет центры кругов (оснований), будем называть осью. Она, в свою очередь, всегда параллельна его образующим.

Как вычислить площадь цилиндра в математике

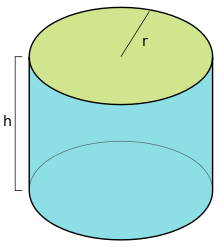Цилиндры бывают различных видов. Мы же остановимся на рассмотрении прямого.

В прямом цилиндре основания – круги перпендикулярны к его образующим. Если мы возьмем прямоугольник и будем вращать его вокруг одной из сторон, то получится прямой цилиндр.

Давайте теперь рассмотрим с вами, как же можно вычислить площадь боковой и полной поверхности прямого цилиндра, зная его радиус и длину образующей, а также как рассчитать его объем. Чтобы все это хорошо усвоить в дальнейшем мы будем использовать вместо цилиндра бочку, имеющую форму цилиндра.

И на примере рассмотрим, как найти площадь поверхности и объем нашей бочки. Мы уже говорили, что цилиндрическая поверхность складывается из боковой поверхности цилиндра и поверхности двух его оснований. Так как основания нашей бочки являются кругами, то тут все просто.

Площадь круга, как мы знаем, равна радиусу, возведенному в квадрат и умноженному на число ?. Давайте обозначим радиус основания бочки как r. Так как у нее есть крышка и дно, то площадь поверхности оснований будет равна: 2?r2

Теперь мы найдем площадь боковой поверхности нашей бочки. Давайте обозначим ее высоту как l. Если мы возьмем, разрежем по линии, перпендикулярной крышке и дну, и развернем боковую поверхность нашей бочки, то получим прямоугольник со смежными сторонами l и 2r (диаметр – это два его радиуса).

Площадь этого прямоугольника, как мы знаем из курса планиметрии, будет равна произведению двух его смежных сторон. Соответственно площадь боковой поверхности нашей бочки будет равна произведению высоты и диаметра ее основания (крышки или дна).

Sбок=2lr Итак, площадь поверхности всей бочки будет равна сумме боковой поверхности и площадей крышки дна: Sц=Sбок+ 2?r2=2lr+2?r2=2r(l+r?)

Как вычислить объем цилиндра в математике

Найдем теперь объем нашей бочки. Объем будем считать равным произведению ее высоты и площади одного из оснований (крышки или дна) Vц=l?r2

Вот так просто на примере бочки мы рассмотрели площадь поверхности и объем цилиндра. Таких примеров при возможности можно привести огромное количество.

Например, рассмотреть данную тему на примере вычисления объема нефти в цистерне цилиндрической формы, или найти площадь боковой поверхности банки или кружки цилиндрической формы.

Про цилиндр в математике мы вам объяснили, не так, как в учебнике, все гораздо проще!